08 Feb La evaluación competencial en Matemáticas
La evaluación competencial en Matemáticas
Desde el último cuarto del siglo XX hasta nuestros días, el proceso de enseñanza-aprendizaje ha ido evolucionando y transformándose de un sistema de aprendizaje de conceptos a otro basado en el desarrollo de las competencias. Además, todo este camino ha comportado para nuestro sistema educativo una progresiva y continua integración con los modelos de los países de nuestro entorno. El aprendizaje matemático, pilar estructural del conocimiento, es también protagonista de esta transformación.

APRENDIZAJE POR CONCEPTOS
El alumnado recibe información de forma constante y la incorpora.

APRENDIZAJE POR PROCEDIMIENTO
El alumnado trabaja, participa y empieza a ser el protagonista de su aprendizaje.

APRENDIZAJE POR ACTIVIDADES
El alumnado investiga y formula hipótesis. Participa como actor principal en todo el proceso que da respuesta a una situación.
Ahora, con la implantación de la LOMLOE, esta evolución redefine una nueva estructura curricular del trabajo:

Este esquema describe esencialmente la situación en la que se encuentra este proceso transformador. Así, en un primer paso, se pasó de trabajar por conceptos a hacerlo por procedimientos (LOGSE). Ello implicaba un cambio en el papel del alumnado como protagonista de su aprendizaje, al participar en este activamente, dejando de ser un mero receptor. La evolución de este paradigma ha llevado al aprendizaje a partir de actividades (LOMLOE), en el que ante una situación se inicia un camino de investigación que llevará a un conocimiento nuevo.
Esta nueva realidad precisa de una evaluación coherente con el nuevo paradigma. Y esta será la evaluación competencial. La evaluación clásica estaba basada en el control de contenidos. La nueva evaluación controlará la adecuada adquisición de competencias. Las actividades que
compongan este proceso evaluativo deben responder a esta realidad presentando situaciones matemáticas que permitan comprobar dicha adquisición.
El método de evaluación de las Matemáticas manipulativas
ProDigi - Quinzet Derive
La propuesta híbrida ProDigi proporciona elementos evaluativos tanto para los saberes como para la adquisición de competencias.
La evaluación de los saberes básicos, desglosados en sentidos matemáticos, dará cuenta del dominio del alumnado en lo que se refiere a los indicadores incluidos en cada sentido.
La evaluación de los saberes básicos, desglosados en sentidos matemáticos, dará cuenta del dominio del alumnado en lo que se refiere a los indicadores incluidos en cada sentido.
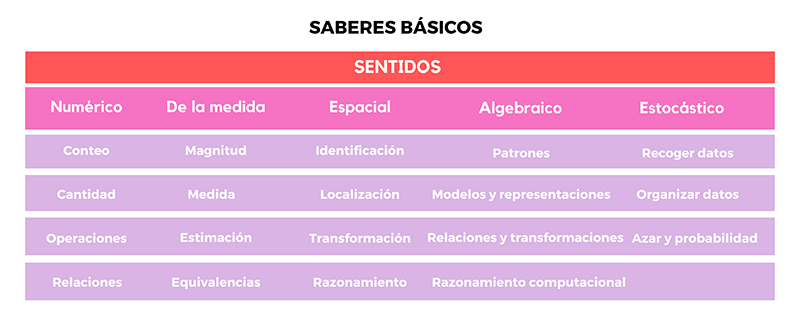
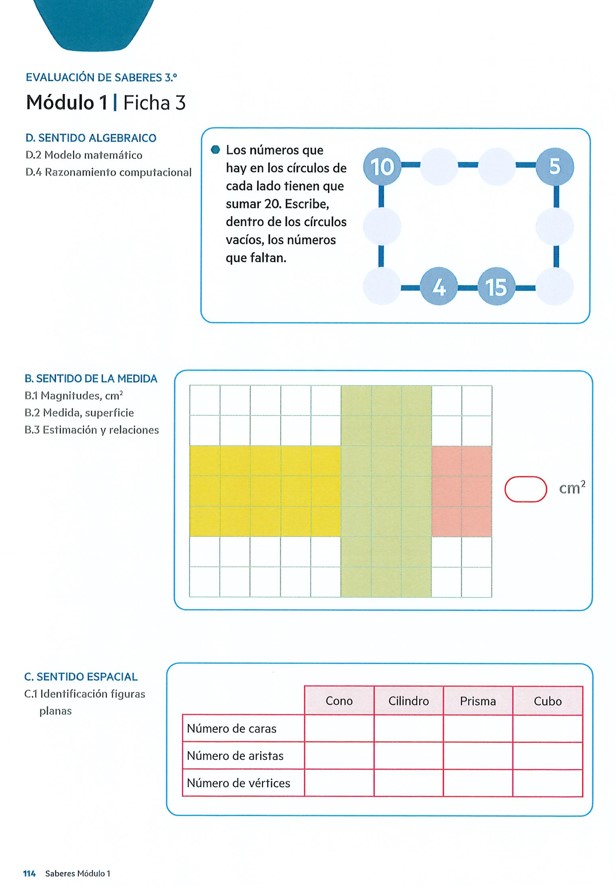
ProDigi proporciona módulos de actividades evaluativas para los seis trimestres del ciclo siguiendo modelos similares a este:
La evaluación de los saberes suele ir ligada a las calificaciones numéricas. En la evaluación por competencias, la calificación numérica no es suficiente y será necesario otro sistema que nos permita controlar los grados de la adquisición competencial.
Habrá que tener claro qué acciones y procesos de aprendizaje se corresponderán con las competencias específicas del currículo.
Habrá que tener claro qué acciones y procesos de aprendizaje se corresponderán con las competencias específicas del currículo.

Por consiguiente, evaluaremos seis competencias matemáticas y dos socioemocionales en situaciones en las que la respuesta implique el trabajo de estas acciones o procesos.
Como pequeño ejemplo de evaluación competencial propondremos una situación en la que intervenga la tabla de los cien primeros números e iniciaremos la serie de acciones en las que deben intervenir las competencias específicas.
Como pequeño ejemplo de evaluación competencial propondremos una situación en la que intervenga la tabla de los cien primeros números e iniciaremos la serie de acciones en las que deben intervenir las competencias específicas.

Podemos empezar preguntando a los alumnos qué ven, qué números creen que podría haber en la tabla.
(INVESTIGAR - COMPETENCIAS 1 y 2)
Sin colocar las tarjetas en la tabla, les preguntaremos cuáles de los números representados en las tarjetas están en la misma fila o en la misma columna y pediremos que justifiquen su respuesta. ) Comprobaremos si la hipótesis formulada es correcta colocando, ahora sí, las tarjetas dentro de la tabla.(CONJETURAR - COMPETENCIAS 3 y 4)
Propondremos que, observando los números de las tarjetas, digan cosas sobre ellos y que conecten el nuevo conocimiento con otras situaciones matemáticas o de su entorno: si son pares, cómo se ordenan, dónde los pueden ver, de qué números son múltiples, si representan unidades o decenas..(CONECTAR - COMPETENCIA 5)
Podemos pedir que expliquen qué saben de la tabla de los cien primeros números, que la describan, que identifiquen cuántas filas o columnas o casillas tiene y que codifiquen esta información pasándola a una hoja de registro.(COMUNICAR Y REPRESENTAR - COMPETENCIA 6)
Todas estas acciones se consignarán en la correspondiente hoja de registro que contiene la competencia específica curricular y la relaciona con los criterios de evaluación y los indicadores de adquisición de cada una.

Para concluir este módulo de evaluación, el método Quinzet Derive propone una evaluación personal. Esta autoevaluación integra la propia conciencia del aprendizaje por parte del alumnado, lo ayuda a conocerse y estimula su deseo de mejora.
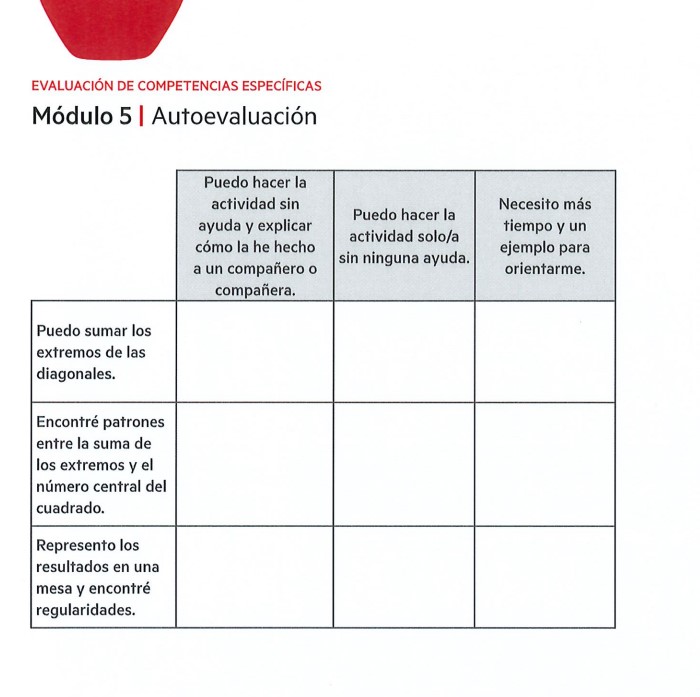
Comparte:
Síguenos:
PUBLICACIONES DESTACADAS
-
Matemáticas. Trabajar a partir de situaciones de aprendizaje
28 junio, 2023 -
Los 5 beneficios de la integración de ProDigi en Classroom
02 junio, 2023 -
Rhythm & Sticks: un juego para el aula de Música
18 mayo, 2023 -
Tecnología al servicio del aprendizaje
04 mayo, 2023






No Comments